Miller Indices - Plane, 밀러지수, 밀러지수 찾는 법

Miller Indices

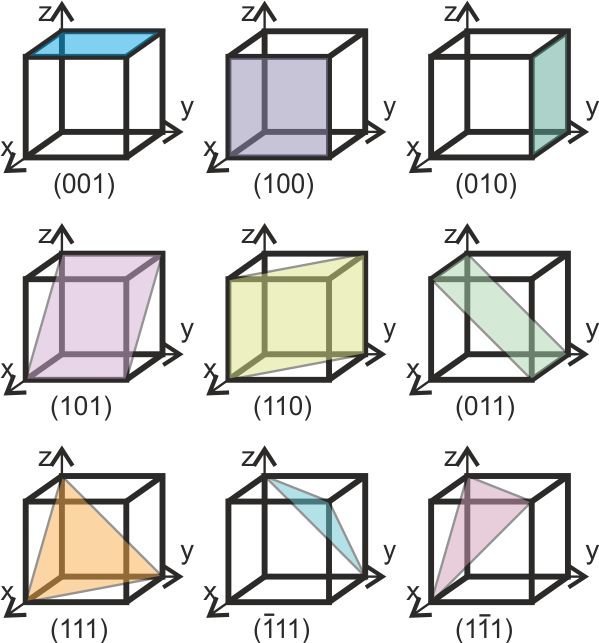
밀러지수 라고하며 결정 면을 표시하는 기호로 x, y,z 축을 어떤 면이 절편을 원자간격으로 측정한 수의 역수 정수비를 (hkl)이라 하는 지수로 나타낸다. 

 

재료공학 과목이나 재료와 관련된 과목들을 배우게 되면 이러한 Miller Indices를 많이 보게 된다. 재료의 구조, Cubic 내에서의 Plane, 재료가 외력을 받을 때 변형이 일어나면서 발생하는 Slip이 실제적으로 일어나는 Slip plane과 같은 결정면들을 표시하기 위해서 많이 사용된다. 그런데 전공서적을 보면 정말 간단한 Plane 들은 이해가 가지만, 조금 복잡한 경우에는 어떻게 해서 이 Plane이 이러한 지수를 가지는지 이해가 되지 않는 경우가 많다. 

 

그래서 어떻게 이러한 지수들을 결정하는지 알아보고 찾아보면서 이해할 수 있도록 하자.

 

 

1. 밀러지수(Miller Indices) 결정 방법

 

다음과 같이 하나의 큐빅이 있다고 생각하고 각 좌표 축을 x,y,z로 두고 시작한다. 여기서는 미리 그림에다가 x,y,z 축을 표기했지만 만일 표기를 하지 않은 경우 표기를 하고 시작하며 다음과 같은 순서대로 찾을 수 있다.

 

1) 각 좌표축(x,y,z) 표시

2) 좌표와 만나는 평면(Plane) 확인

3) 역수를 취하기

4) 정수의 형태를 취하기

 

 

다음과 같은 순서에 따라서 실제로 하나씩 해보자.

 

 

 

 

 

1) 각 좌표축(x,y,z) 표시

 

이미 그림에서 x,y,z 표시를 했기 때문에 생략하도록 하겠다.

 

2) 좌표와 만나는 평면(Plane) 확인

 

예를 들어서 다음 그림과 같이 Cubic의 상단 부분의 평면의 밀러지수를 찾는다고 가정해보자.

여기서 주목해야 할 점은 녹색으로 칠해진 평면이 어떤 축과 만나는 지 알아보는 것이다. 그림에서는 녹색의 평면이 어떤 축과 만나는가(교차하는가)?  x, y축과는 평행해서 영원히 만날 수 없게 되고, 그림 상에서는 z 축과 만나게 된다. 그럼 이 평면을 구할 때는 z 축과 만나는 것을 인지한다. 그러면 진짜 밀러지수를 구하기 전, 임시 상태의 intercept 좌표를 구한다. 

x,y 축과는 만나지 않기 때문에 ∞로 표시하고, z축은 1로 표시한다. 하나의 단일 Cubic에서의 한 변의 길이를 1이라고 가정한다. 그러면 [∞,∞,1]로 임시적으로 표시가 가능하다.

 

 

3) 역수를 취하기

 

Step 2에서 구했던 [∞,∞,1]을 그대로 역수를 취해준다. 그러면 다음과 같이 구할 수 있다. [1/∞, 1/∞, 1/1], 즉 [0,0,1]로 구할 수있으며 색칠한 평면의 밀러지수는 [001]으로 결정된다.

 

 

4) 정수의 형태를 취하기

 

여기서는 이미 [001] 이라는 정수의 형태로 나왔기 때문에 따로 해 줄 것이 없다.

 

조금 더 다른 예시를 한번 보고 연습하고 적용해보면 더욱 더 이해도 되고 어려움이 없을 것이다. 

 

 

이 평면의 밀러지수는 어떻게 구해야할까? 평면이 1/2 지점에 위치하고 있다고 가정한다. 이 문제의 경우에 평면과 만나는 축은 역시나 z 축 뿐이다. 하지만 높이는 1/2 지점이다. 그러면 임시의 밀러지수는 [∞,∞,1/2]가 될 것이다. 이 값에서 역수를 취해주면 [1/∞,1/∞,2]가 되므로 밀러지수는 [002]로 결정할 수있다.

 

조금 더 다른 예시를 한번 더 살펴보자.

 

이 문제의 경우에 평면이 위치하는 곳이 조금 다르다. 우선 파악해보면 평면이 x,z 축과 만나고 있으며 원점(0,0,0)인 O와도 만나고 있다. 따라서 이러한 경우에는 원점을 살짝 이동시켜주어서 문제를 해결한다. 기존에 지정했던 원점과 평면이 만나는 상태로 있게 된다면 항상 원점을 이동시켜서 문제를 풀어주어야 한다.

 

새로운 원점을 O' 으로 그림과 같이 변경해주었다. 그리고 원점이 이동함에 따라 축도 함께 이동해주었다. 이러한 관점에서 보게되면 구하고자하는 빨강 평면은 y축과만 교차하고 있는 셈이 된다. 그러면 x,z축과는 만나지 않는다. 여기서 하나 주의할 점은 원점을 기준으로 -1 지점에 평면이 있으니 y 좌표를 -1로 인식해 주는 것이다. 그러면 임시좌표를 다음과 같이 구해진다

 

[∞,-1,∞]

 

이를 다시 역수로 취해주면 

 

[0,-1,0]

 

 

이런식으로 구할 수 있게 된다. 그러면 연습할 그림을 보고 올바르게 구할 수 있는지 확인해보자.

 

 

정답은 다음과 같다.

 

Plane	임시좌표(intercept)	Indices
A	∞,∞,1	(0 0 1)
B	1,1,1	(1 1 1)
C	1,∞,1/2	(1 0 2)
D	∞,∞-1	(0 0 -1)

 

 

밀러지수가 나올 때 마다 어떻게 평면의 밀러지수가 이렇게 되지? 라고 고민했던 적이 많은데, 이렇게 결정하는 방법을 확인 후 보면 헷갈리지 않고 도움이 될 수 있을 것이다.